Enzyme inhibitors are molecules that reduce or abolish enzyme activity. These are either reversible (i.e., removal of the inhibitor restores enzyme activity) or irreversible (i.e., the inhibitor permanently inactivates the enzyme).
Reversible inhibitors
Reversible enzyme inhibitors can be classified as competitive, uncompetitive, non-competitive or mixed, according to their effects on Km and Vmax. These different effects result from the inhibitor binding to the enzyme E, to the enzyme–substrate complex ES, or to both, as shown in the figure to the right and the table below. The particular type of an inhibitor can be discerned by studying the enzyme kinetics as a function of the inhibitor concentration. The four types of inhibition produce Lineweaver–Burke and Eadie–Hofstee plots[39] that vary in distinctive ways with inhibitor concentration. For brevity, two symbols are used:
![\alpha = 1 + \frac{[\mbox{I}]}{K_{i}}](http://upload.wikimedia.org/math/5/d/0/5d0ef5c67ccd4c852e6cfca33a00b3c1.png) and
and ![\alpha^{\prime} = 1 + \frac{[\mbox{I}]}{K_{i}^{\prime}}](http://upload.wikimedia.org/math/1/3/1/131b809d1c25e2a337f97992bbbc9593.png)
where Ki and K'i are the dissociation constants for binding to the enzyme and to the enzyme–substrate complex, respectively. In the presence of the reversible inhibitor, the enzyme's apparent Km and Vmax become (α/α')Km and (1/α')Vmax, respectively, as shown below for common cases.
| Type of inhibition | Km apparent | Vmax apparent | ||
| Ki only | ( ) ) | competitive | 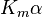 | 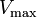 |
| Ki' only | (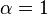 ) ) | uncompetitive | 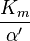 | 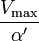 |
| Ki = Ki' | (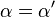 ) ) | non-competitive | 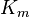 | 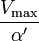 |
| Ki ≠ Ki' | (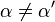 ) ) | mixed |  | 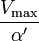 |
Non-linear regression fits of the enzyme kinetics data to the rate equations above[40] can yield accurate estimates of the dissociation constants Ki .